NOVIEMBRE

FUNCIONES DE VARIAS VARIABLES.

Se estudian las funciones desde los siguientes puntos de vista:

-Verbalmente (mediante una descripción hecha con palabras).

-Numéricamente (mediante una tabla de valores).
-Algebraicamente (mediante una fórmula explícita).

-Visualmente (mediante una gráfica o curvas de nivel).

• Representación Gráfica de una función.-
  
  
• Graficando en el espacio:
  
  
  
  
  
  DOMINIO DE DEFINICIÓN O CAMPO DE EXISTENCIA
  
  
  
  El dominio donde f(x,y) existe es una región del plano XOY o todo el plano XOY.
  
  Análisis del Dominio de Definición.
  
  
  Análisis Matemático
  
  Análisis Gráfico
  
  Análisis Descriptivo

EJEMPLO:
Determine el dominio, rango y gráfica de :

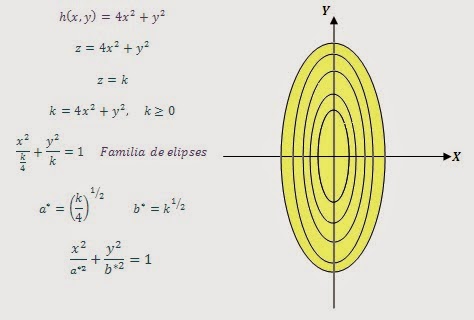
CURVAS DE NIVEL

Las curvas de nivel de una función f (x,y), son las curvas cuyas ecuaciones son f (x,y) = k, donde "k" es una constante en el rango de f (x,y).

EJEMPLO:

CURVAS DE CONTORNO
Es la representación de las curvas de nivel en R3.

SUPERFICIE DE NIVEL





EJEMPLO: Las capas del planeta Tierra.



HIPERSUPERFICIE DE NIVEL

LIMITES

Observaciones:


1. Si por dos caminos o trayectorias el valor del limite tiene un valor diferente, entonces se concluye que NO existe el limite.
2. Si por dos camino o trayectorias el valor del limite tiene el mismo valor se supone que el limite existe y se debe proceder a demostrar su existencia.
3. Los caminos elegidos para evaluar el limite deben contener al punto (a,b) de interés.


DEMOSTRACIÓN LIMITES

NOTA:
La demostracion de los limites se puede realizar de dos maneras distintas con: coordenadas polares y mediante la definicion.

OPERACIONES LIMITES




CONTINUIDAD: Se dice que f (x,y) es continua en (a,b) si se cumple:

NOTA:
Si no se cumple alguna de las condiciones entonces se dice que f (x,y) es discontinua en (a,b) y puede ser:

1. Discontinua Inevitable:


2. Discontinua Evitable:

Toda discontinuidad evitable se debe redefinir.


DERIVADAS PARCIALES

Observaciones:

1. Cuando derivamos parcialmente con respecto a "x",la variables "y" se asume como constante.
2. Cuando derivamos parcialmente con respecto a "y", la variable "x" se asume como constante.
3. Se aplican todas las reglas de derivación de las funciones de una sola variable.

INTERPRETACIÓN GEOMÉTRICA DE LAS DERIVADAS PARCIALES

INTERPRETACIÓN FÍSICA1. Las derivadas parciales de z = f(x,y) representan las Razones de Cambio de la variable z cuando "x" varia manteniendo fijo "y". En el otro caso, la Razón de cambio de z cuando "y" varia manteniendo fijo "x".

2. Se puede hablar de etapas o indices de cambio.

PLANOS TANGENTESSupongamos que f(x,y) f tiene derivadas parciales de primer orden continuas. Entonces el plano tangente a la superficie z=f(x,y) en el punto P(a,b,f(a,b)) es el plano que pasa por P que contiene las recta tangentes a las dos curvas.

DERIVADAS DE ORDEN SUPERIOR

Si z = f(x,y) entonces existen 4 derivadas parciales de segundo orden, 8 derivadas parciales de tercer orden....

Si w = f(x,y,z) entonces existen:

Si las derivadas parciales son continuas, entonces las derivadas cruzadas son iguales: